Electroencephalography source localization

Article information

Clin Exp Pediatr. 2023;66(5):201-209

Publication date (electronic) : 2022 December 29

doi : https://doi.org/10.3345/cep.2022.00962

Department of Pediatrics, College of Medicine, The Catholic University of Korea, Seoul, Korea

Corresponding author: Tae-Hoon Eom, MD, PhD. Department of Pediatrics, College of Medicine, The Catholic University of Korea, Seoul, Korea Email: good1976@hanmail.net

Received 2022 July 21; Revised 2022 November 4; Accepted 2022 November 7.

See editorial "Understanding the usefulness of electroencephalography source localization" in Volume 66 on page 210.

Abstract

Electroencephalography (EEG) has been and is still widely used in brain function research. EEG has advantages over other neuroimaging modalities. First, it not only directly images the electrical activity of neurons; it has a higher temporal resolution. Furthermore, current advanced technologies enable accurate mathematical calculations and sophisticated localization from EEG data. Several important factors should be considered for EEG analysis using these advanced technologies. First, raw EEG data contain physiological or nonphysiological artifacts. Therefore, preprocessing methods and algorithms to detect and remove these artifacts have been proposed and developed. In the analysis of preprocessed EEG, forward and inverse problems require solving and several proposed models have been applied. To solve the forward problem, the source information and matrix parameters from which the EEG originates are essential. Therefore, an accurate head model is required. In contrast, the possible combinations of the current sources computed inversely from EEG measured at a limited number of electrodes are infinite, referring to the inverse problem. The inverse problem can be solved by setting limits based on assumptions made of the anatomy and physiology on the generation and propagation of the current sources. Thus, methods such as dipole source models and distributed source models have been proposed. Source localization requires the consideration of many factors such as the preprocessing of raw EEG data, artifact removal, accurate head models and forward problems, and inverse computation problems. This review summarizes the methods and considerations applied to the above EEG source localization process. It also introduces the applications of EEG source localization for epilepsy and other diseases as well as brain function studies and discusses future directions.

Keywords: Electroencephalography; Source localization; Dipole source model; Distributed source model

Key message

· Electroencephalography (EEG) directly images the electrical activity of neurons at a higher temporal resolution than other neuroimaging techniques.

· EEG is still widely used in brain function research due to its advantages.

· Forward and inverse problems of EEG analyses require solutions.

· Methods such as the dipole and distributed source models have been introduced.

· Applications of EEG are expanding with the integration of other technologies and large-scale data.

Introduction

Electroencephalography (EEG) has traditionally been used to study brain function. However, brain function has also been studied using single photon emission computed tomography (SPECT) and positron emission tomography (PET). More recently, functional magnetic resonance imaging (fMRI) and magnetic encephalography (MEG) were introduced. PET, SPECT, and fMRI image secondary hemodynamic and metabolic changes in neuronal electrical activity, whereas EEG and MEG directly image neuronal electromagnetic activity [1]. EEG and MEG have the additional advantage of superior temporal resolution compared to PET, SPECT, and fMRI [1,2]. However, EEG and MEG have limited spatial resolution. Thus, many source analysis techniques have been introduced to improve its spatial resolution (Fig. 1) [1,3].

Fig. 1.

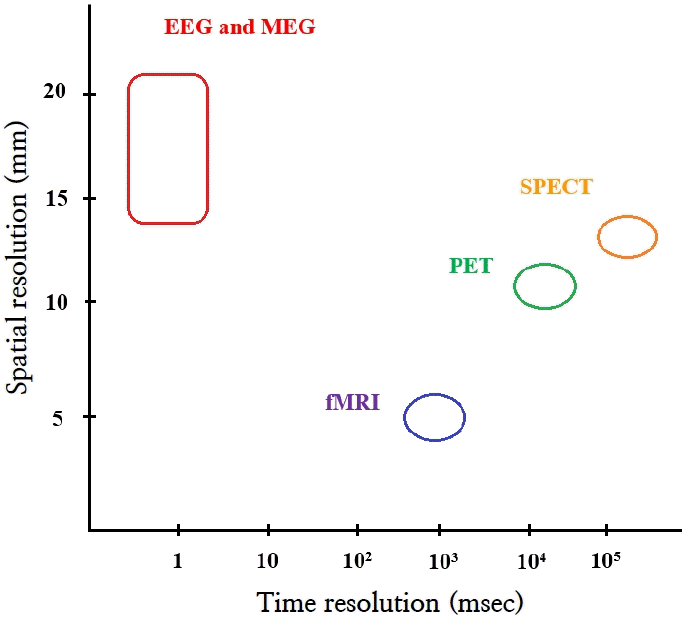
Temporal and spatial resolutions of neuroimaging modalities. EEG, electroencephalography; fMRI, functional magnetic resonance imaging; MEG, magnetic encephalography; PET, positron emission tomography; SPECT, single photon emission tomography.

EEG is still widely used in brain function research due to being much easier to implement than MEG and not requiring specialized equipment. Recent source localization methods have enabled accurate mathematical calculations and sophisticated localization from EEG data. Source localization refers to inferring the distribution of current sources from measured EEG data. However, there are many considerations in proper use of EEG for brain function studies along with recent source analysis techniques. These include the preprocessing of raw EEG data, artifact removal, accurate head models and forward problems, and inverse computation problems. This review introduces the basic concepts, technical methods, and application of source analysis using EEG.

EEG recordings

EEG, which measures the electrical activity of the brain, is divided into invasive and noninvasive EEG according to the attachment site of the measuring electrodes [4]. In the clinical and research fields, noninvasive EEG is commonly used in which electrodes are attached to the scalp by the international 10–20 system to evenly reflect activity across the brain (Fig. 2) [5,6]. The 10–20 system is the international standard used to localize the scalp electrodes. This is an important component in analyses of the localization and distribution in the source analysis of EEG. Regarding the number of electrodes used, 8–21 channels are applied in clinical practice, whereas up to to 256 channels are sometimes applied for research purposes [4,7,8].

Fig. 2.

Electrode locations of International 10–20 system.

EEG is induced by a potential difference of about 100 mV between the cell membranes of the axons caused by the excitation of pyramidal cells in the cerebral cortex [1]. These pyramidal cells are oriented perpendicular to the surface of the cerebral cortex. The summation of the postsynaptic action potentials by the action potential of each neuron is measured at each electrode through the matrix of the meninges, cerebrospinal fluid, skull, and scalp. Since the potentials measured at the electrodes are very low, the use of an amplifier to record them is required. EEG is an electrical wave that features period, frequency, amplitude, and phase components. EEG is divided into delta (0.5–3 Hz), theta, (4–7 Hz), alpha (8–13 Hz), beta (14–30 Hz), and gamma (≥30 Hz) waves according to frequency, and the recorded EEG can be considered the sum of waves with various frequencies and amplitudes [9,10].

Raw EEG data and preprocessing

EEG is visually inspected in clinical practice, through which abnormalities such as epileptiform discharges are detected and current sources in the brain are inferred. However, to accurately analyze the current sources, the potentials measured on the scalp and their coordinates should be calculated mathematically [11]. Raw EEG data are analyzed using a computer. The raw EEG file contains the potentials of each channel recorded over time. Raw EEG data can be viewed in the form of a 2-dimensional array of channel × time. These raw EEG data can also be converted into signals in the frequency domain through Fourier transformation, the decomposition of signals defined in the time domain into sine and cosine functions at various frequencies. Each sine and cosine function has its own frequency and amplitude (Fig. 3).

Fig. 3.

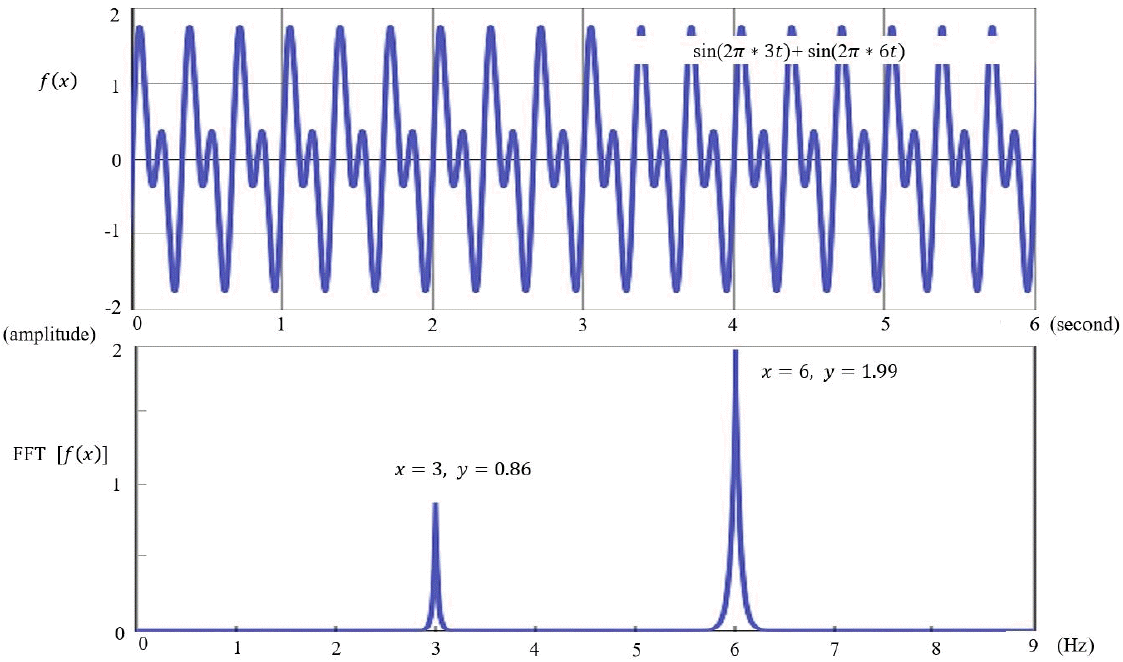
Fast Fourier transform (FFT) time and frequency domain. FFT is the decomposition of signals defined in the time domain into sine and cosine functions with various frequencies.

The raw EEG data require preprocessing prior to analysis. Raw EEG data are often contaminated by electrical activities not originating in the brain. These artifacts include physiologic (e.g., electromyography, electrocardiography, eye movements, respiration, and body movements) and nonphysiologic (e.g., electrode artifacts, power lines, and other medical devices). These artifacts should be preprocessed prior to analysis, which involves visual inspection by experienced electrophysiologists [12]. In addition, the automatic detection and removal of artifacts provided by analysis software can be implemented [13]. These preprocessing methods apply techniques such as filtering methods, wavelet transforms, and independent component analysis (ICA) [4,14-16].

Head models

The potentials and distributions in EEG measured on the scalp can be accurately determined when the initial source information and matrix parameters from which the EEG originates are known [11]. This is related to a forward problem in EEG analysis, for which an accurate head model is required to solve. Reconstruction of the head model requires variables including head shape and size and the electrical conductivity of its components (scalp, skull, meninges, and cerebrospinal fluid). Thus, an individualized magnetic resonance image (MRI) is recommended as a head model [12]. If not available, a known MRI template can be used; in such cases, the Montreal Neurological Institute (MNI template) is widely used. The MNI template uses MRI data from 152 young adults (18–43.5 years old) from the MNI by the International Consortium for Brain Mapping. However, the use of a standard template rather than an individualized MRI results in less accurate analysis results. Moreover, there are particular limitations to its use in children, for whom age-specific standard templates are required (Fig. 4) [17].

Fig. 4.

International Consortium for Brain Mapping 152 Nonlinear atlases (2009). CSF, cerebrospinal fluid; GM, gray matter; PDw, proton density-weighted; T1w, T1-weighted; T2w, T2-weighted; WM, white matter. Adapted from: http://nist.mni.mcgill.ca/icbm-152-nonlinear-atlases-2009/. Copyrightⓒ1993–2004 by Louis Collins, McConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University.

Inverse problem

In the process of identifying the current sources in the brain from the potentials and distribution measured by EEG electrodes on the scalp, the number of combinations of the current sources generating the potentials and distribution measured by a certain number of electrodes may be infinite [1,11]. This is the inverse problem that can be solved by setting limitations using assumptions based on the anatomy and physiology of the generation and propagation of the current sources [1,11,18,19]. To solve this problem, many proposals have been introduced, and the proposed models and technical methods have been improved and validated [11,18,20]. Thus, the source analysis model of the dipole source localization and distributed source localization, which are currently widely used, are summarized here.

Dipole source localization

Dipole source localization was a model proposed early to solve the inverse problem in EEG analysis [1,11,18,21,22]. The cell bodies and apical dendrites of the neuron form current dipoles with opposite charges. A constraint assumed in this model is that a limited number of current dipoles consisting of anodes and cathodes at both ends in the brain produce potential fields measured by the scalp electrodes. This model is a simple and useful method that schematizes electrophysiological mechanisms of a measured EEG [23,24]. Dipole source localization is performed by calculating the location, direction, and moment parameters of the assumed number of current dipoles. The direction of the current dipole may be tangential or radial to the brain surface. Therefore, even dipoles at the same location differ in the potential field formed on the scalp by direction [11]. Given these constraints, the current source localization is mathematically solved by nonlinear optimization [21,25]. If the location of the current source is known a priori, the direction and moment of the current source can be calculated by linear optimization [21]. There are 2 approaches to dipole source localization [1,11,26]. Single time-slice localization is the method of applying the dipole source model to each time point and is mainly used for the source localization of event-related potential or epileptiform discharge [27,28]. Another approach is multiple time-slice localization, which fixes the locations or locations/directions of a limited number of current dipoles and calculates changes in the potential of current dipoles over a certain period [25,29].

Determining the number of current sources in dipole source localization is an important issue. Dipole source localization is useful if the number of current sources is known or a limited number of current dipoles can be assumed (e.g., in patients with epilepsy) [30,31]. The number of current sources can be determined by the multiple source search algorithm provided by the analysis software, which finds the appropriate number of current sources through nonlinear or linear/nonlinear optimization [18,25,32]. However, the use of dipole source localization is limited because the number of current sources is not always known or cannot be assumed [1,11]. Moreover, if the limited number of current sources is under- or overestimated, the source analysis will be biased or inaccurate [18]. However, dipole source localization is still widely used in certain situations where the number of current sources is known or can be assumed a priori [1,18].

Distributed source localization

Distributed source localization reconstructs the 3-dimensional structure of the brain into numerous lattice points (usually more than 5,000) and presents a model in which current dipoles located in each lattice are distributed in their respective strengths [11,18]. Therefore, it is unnecessary to determine or assume the number of current sources. However, the number of lattice points in the distributed source model is much higher than the number of electrodes measured on the scalp; thus, this inverse problem requires solving [1,18]. In the head model, the lattice locations are limited to gray matter and the hippocampus using individual or template MRI, and the restrictions by this anatomical information reduce the number of variables [11,18]. Moreover, in the distributed source model, a minimum norm (MN) approach is proposed that assumes the appropriateness of a distribution minimizing the total energy of each current source [33]. Here the MN solution tends to be close to the scalp electrodes and overlooks deep brain current sources [1,11]. Therefore, a depth-weighted MN approach has been proposed to compensate for this disadvantage. However, the depth-weighted MN solution features lower resolution [34-37].

Distributed source models are now widely used and increasingly sophisticated. LORETA software uses the Laplacian-weighted MN approach, which assumes that neighboring neuronal activities are correlated; thus, the current density distribution is smoothed. However, LORETA software has the disadvantage of producing blurred and over-smoothed images [38]. LORETA has been updated to sLORETA (and more recently eLORETA) to compensate for these shortcomings [39,40]. VARETA and LAURA have also been introduced by other research groups [41,42]. Moreover, a spatiotemporal source method (Beamforming) based on the assumption that neuronal activities are temporally as well as spatially correlated was introduced, and ICA was applied to localize each independent component and recombine them [43].

Applications of EEG source localization

EEG source localization has been widely used in brain research, and many studies are currently underway in various fields. More recent tools, such as fMRI, have been introduced and actively used in neuroimaging research, but EEG has its own advantages as mentioned above. In addition, the application of high-density EEG and many electrodes is readily available clinically and in research settings, and source localization methods have been further developed [12]. Therefore, EEG source localization is increasingly being used to explore brain regions associated with brain function and neurological disorders [2,18,44-46].

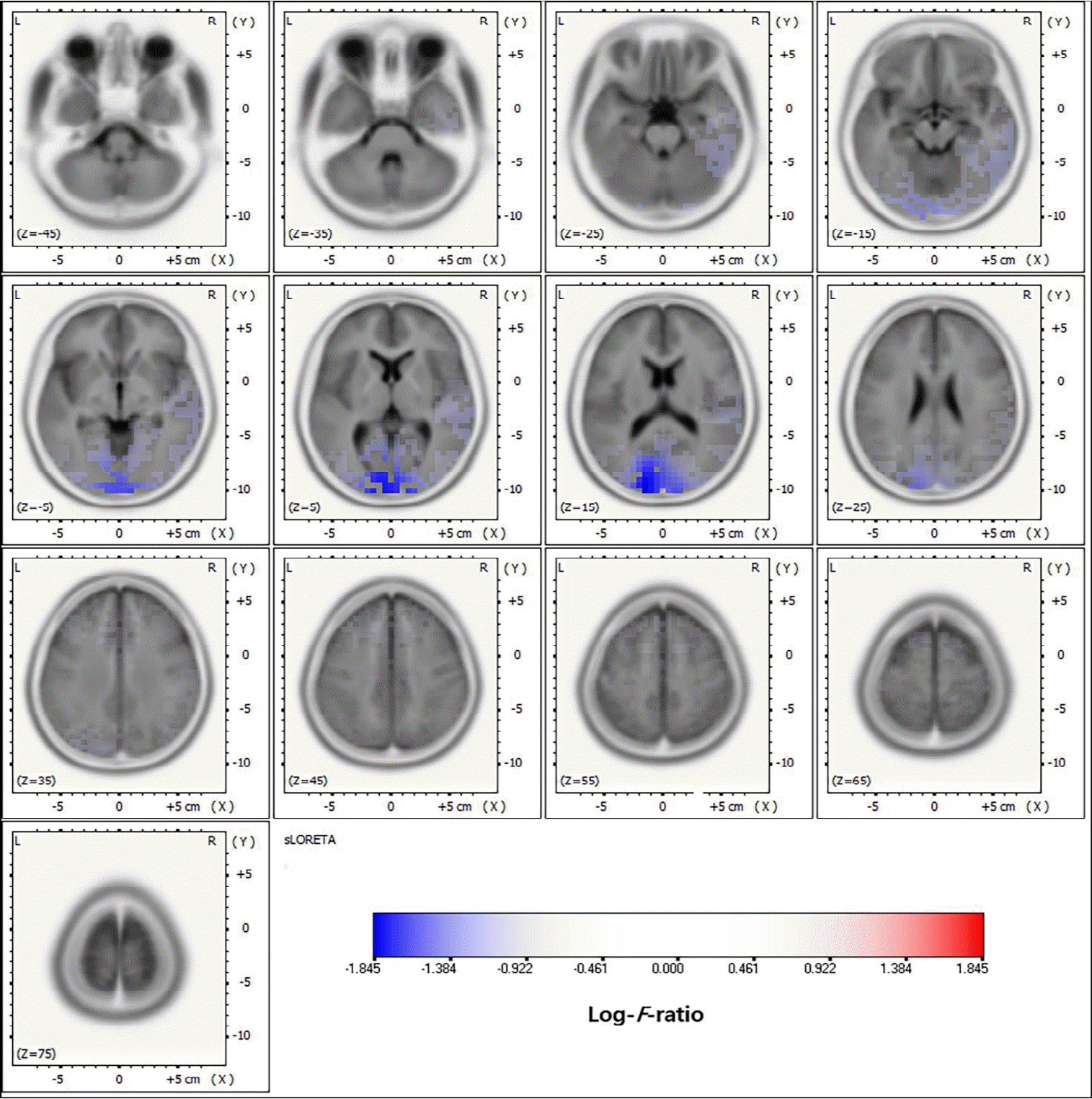
EEG source localization has been most commonly applied in patients with epilepsy, particularly to localize the epileptic focus in focal epilepsy [47,48]. The application of EEG source localization to presurgical evaluations in epilepsy can prove its accuracy and usefulness by comparison with intracranial EEG and surgical outcomes [49-52]. The dipole source model was initially applied to localize the epileptic focus in epilepsy surgery, and its accuracy was demonstrated by comparison to intracranial EEG and surgical outcomes [26,27]. The dipole source model has been well described, especially in studies of temporal lobe epilepsy and benign childhood epilepsy with centrotemporal spikes in pediatrics [53,54]. However, in multifocal epilepsy with multiple electrical sources, the dipole source model has limited application [55-57]. Subsequently, distributed source localization has also been applied in patients with epilepsy and was proven accurate in many studies (Fig. 5). Studies of large-scale epilepsy patients reported higher sensitivity and specificity compared to PET and SPECT [17,58]. High-density EEG and individual MRI as head models ensured this accuracy, but the application of low-density EEGs and template MRIs showed limited accuracy. Several commercial EEG analysis software packages are currently being used to localize the epilepsy focus in epilepsy surgery with intracranial EEG recording and guide the location of intracranial EEG electrodes [18].

Fig. 5.

Distributed source localization in juvenile myoclonic epilepsy. Adapted from Moon, et al. BMC Neurol 2022;22:48 [58].

EEG source localization is also applied in neurological and psychiatric diseases other than epilepsy [12]. Such localization has been most often applied in research and clinical studies of attention deficit disorder with hyperactivity (ADHD). ADHD is associated with abnormal frontal lobe function of inhibitory control and attention, for which EEG source localization has been applied to many studies. Several EEG source localization studies in ADHD patients have reported abnormalities in the frontal lobe and associated brain networks [59,60]. Moreover, EEG source localization plays an important role in the analysis of quantitative EEG, which was introduced and applied in clinical practice [61]. EEG source localization has also been applied in many neurological and psychiatric disorders, such as anxiety disorders, obsessive-compulsive disorder, and sleep disorders [18]. It is useful for identifying relevant brain regions in terms of neuroanatomy and physiology in brain function research. The application field is very diverse and is expanding (Table 1) [53,58,62-69].

Table 1.

Overview of recent EEG source localization studies [53,58,62-69]

Future directions

EEG source localization is increasingly expanding in application and continues to evolveevolve (Table 2) [70-77]. Multimodal methods, such as the integration of the high temporal resolution of EEG and high spatial resolution of fMRI, can be a promising approach. Higher spatiotemporal resolution is being demanded in neuroimaging research, and this multimodal method may be a good alternative [78]. In addition, the combination of EEG-MEG and EEG– functional near-infrared spectroscopy may provide further information in brain function research [4,79]. Along with real-time EEG monitoring, EEG source localization can be applied to the brain-computer interface, which is implemented by analyzing signals obtained from the brain and transmitting them to a computer [70,80,81]. Although many challenges require addressing, EEG source localization is expected to play an important role in brain signal analyses. Numerous neuroimaging studies are currently underway and data on EEG localization being published, but the data from these studies requires unification and integration into big data in the future, which requires the standardization of research protocols and measurement methods [71,80,82]. These tasks may be very challenging, but they can enable more advanced knowledge and technologies. A machine learning algorithm can also be applied to EEG source localization [83-85]. Such EEG source localization studies have recently been reported and are showing promising results. The introduction of these recent technologies is providing new insight into EEG research and brain function.

Table 2.

Overview of EEG source localization studies in promising fields [70-77]

Conclusions

This review described the steps applied in the process of EEG source localization and their basic concepts and considerations. EEG analysis and application techniques are being increasingly developed, so EEG analysis research is expected to be more widely implemented in the future. Although the technical details of EEG analysis may be unfamiliar to clinicians, EEG source localization can provide new insight into brain function in clinical practice; therefore, increased understanding is required. Moreover, the applications of EEG source localization are expanding with its integration with other technologies and largescale data, and EEG analysis will continue to be a promising field of functional neuroimaging research.

Notes

Conflicts of interest

No potential conflict of interest relevant to this article was reported.

Funding

This work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT; Ministry of Science and ICT) (no. 2020R1G1A1099968).

References

1. He B, Sohrabpour A, Brown E, Liu Z. Electrophysiological source imaging: a noninvasive window to brain dynamics. Annu Rev Biomed Eng 2018;20:171–96.

2. Asadzadeh S, Yousefi Rezaii T, Beheshti S, Delpak A, Meshgini S. A systematic review of EEG source localization techniques and their applications on diagnosis of brain abnormalities. J Neurosci Methods 2020;339:108740.

3. Lopes da Silva F. EEG and MEG: relevance to neuroscience. Neuron 2013;80:1112–28.

4. Martinek R, Ladrova M, Sidikova M, Jaros R, Behbehani K, Kahankova R, et al. Advanced bioelectrical signal processing methods: past, present and future approach- Part II: brain signals. Sensors (Basel) 2021;21:6343.

5. Jurcak V, Tsuzuki D, Dan I. 10/20, 10/10, and 10/5 systems revisited: their validity as relative head-surface-based positioning systems. Neuroimage 2007;34:1600–11.

6. Ball T, Kern M, Mutschler I, Aertsen A, Schulze-Bonhage A. Signal quality of simultaneously recorded invasive and non-invasive EEG. Neuroimage 2009;46:708–16.

7. Oostenveld R, Praamstra P. The five percent electrode system for highresolution EEG and ERP measurements. Clin Neurophysiol 2001;112:713–9.

8. Ferree TC, Luu P, Russell GS, Tucker DM. Scalp electrode impedance, infection risk, and EEG data quality. Clin Neurophysiol 2001;112:536–44.

9. Fink A, Grabner RH, Neuper C, Neubauer AC. EEG alpha band dissociation with increasing task demands. Brain Res Cogn Brain Res 2005;24:252–9.

10. Chervin RD, Burns JW, Subotic NS, Roussi C, Thelen B, Ruzicka DL. Correlates of respiratory cycle-related EEG changes in children with sleep-disordered breathing. Sleep 2004;27:116–21.

11. Kwon OY. Current source analysis of electroencephalography. Hanyang Med Rev 2006;26:61–8.

12. Michel CM, Brunet D. EEG source imaging: a practical review of the analysis steps. Front Neurol 2019;10:325.

13. Pernet CR, Garrido M, Gramfort A, Maurits N, Michel C, Pang E, et al. Best practices in data analysis and sharing in neuroimaging using MEG. OSF Preprints [Preprint] 2018;[cited 2020 Jul 1]. Available from: osf.io/a8dhx.

14. Cichocki A, Rutkowski T, Siwek K. Blind signal extraction of signals with specified frequency band. In : Proceedings of the 12th IEEE workshop on neural networks for signal processing; 2002 Sep 6; Martigny, Switzerland; 2002. 515–24.

15. Gallego-Jutglà E, Solé-Casals J, Rutkowski TM, Cichocki A. Application of multivariate empirical mode decomposition for cleaning eye blinks artifacts from EEG signals. In : Proceedings of the International Conference on Neural Computation Theory and Applications (special session on Challenges in Neuroengineering-2011). Setúbal (Portugal). Science and Technology Publications, Lda. 2011. 455–60.

16. Rakhmatulin I. Review of EEG feature selection by neural networks. Int J Sci Bus 2020;4:101–12.

17. Brodbeck V, Spinelli L, Lascano AM, Wissmeier M, Vargas MI, Vulliemoz S, et al. Electroencephalographic source imaging: a prospective study of 152 operated epileptic patients. Brain 2011;134:2887–97.

18. Michel CM, He B. EEG source localization. Handb Clin Neurol 2019;160:85–101.

19. Fender D. Source localization of brain electrical activity. In : Rémond A, ed. Methods of analysis of brain electrical and magnetic signals Amsterdam: Elsevier Science; 1987. p. 335–403.

20. Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, Grave de Peralta R. EEG source imaging. Clin Neurophysiol 2004;115:2195–222.

21. He B, Musha T, Okamoto Y, Homma S, Nakajima Y, Sato T. Electric dipole tracing in the brain by means of the boundary element method and its accuracy. IEEE Trans Biomed Eng 1987;34:406–14.

22. Scherg M, Von Cramon D. Two bilateral sources of the late AEP as identified by a spatio-temporal dipole model. Electroencephalogr Clin Neurophysiol 1985;62:32–44.

23. Ebersole JS. Cortical generator and EEG voltage fields. In : Ebersole JS, Pedly TA, eds. Current practice of clinical electroencephalography 3rd edth ed. Philadelphia (PA): Wolters Kluwer Health; 2003. p. 12–31.

24. Gloor P. Neuronal generators and the problem of localization in electroencephalography: application of volume conductor theory to electroencephalography. J Clin Neurophysiol 1985;2:327–54.

25. Scherg M, von Cramon D. A new interpretation of the generators of BAEP waves I-V: results of a spatio-temporal dipole model. Electroencephalogr Clin Neurophysiol 1985;62:290–9.

26. Ebersole JS. EEG dipole modeling in complex partial epilepsy. Brain Topogr 1991;4:113–23.

27. Ebersole JS, Wade PB. Spike voltage topography and equivalent dipole localization in complex partial epilepsy. Brain Topogr 1990;3:21–34.

28. Wong PK. Potential fields, EEG maps, and cortical spike generators. Electroencephalogr Clin Neurophysiol 1998;106:138–41.

29. Scherg M. Functional imaging and localization of electromagnetic brain activity. Brain Topogr 1992;5:103–11.

30. Ebersole JS, Hawes S, Scherg M. Intracranial EEG validation of spike propagation predicted by dipole models. Electroencephalogr Clin Neurophysiol 1995;95:18–9.

31. Lantz G, Holub M, Ryding E, Rosén I. Simultaneous intracranial and extracranial recording of interictal epileptiform activity in patients with drug resistant partial epilepsy: patterns of conduction and results from dipole reconstructions. Electroencephalogr Clin Neurophysiol 1996;99:69–78.

32. Mosher JC, Lewis PS, Leahy RM. Multiple dipole modeling and localization from spatio-temporal MEG data. IEEE Trans Biomed Eng 1992;39:541–57.

33. Hämäläinen MS, Ilmoniemi RJ. Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput 1994;32:35–42.

34. Wang JZ, Williamson SJ, Kaufman L. Magnetic source images determined by a lead-field analysis: the unique minimum-norm least-squares estimation. IEEE Trans Biomed Eng 1992;39:665–75.

35. Lawson CL, Hanson RJ. Solving least squares problems Philadelphia (PA): Society for Industrial and Applied Mathematics; 1995.

36. Greenblatt RE. Probabilistic reconstruction of multiple sources in the bioelectromagnetic inverse problem. Inverse Probl 1993;9:271–84.

37. Fuchs M, Wischmann HA, Wagner M. Generalized minimum norm least squares reconstruction algorithms. ISBET Newsl 1994;5:8–11.

38. Pascual-Marqui RD, Michel CM, Lehmann D. Low resolution electromagnetic tomography: a new method for localizing electrical activity in the brain. Int J Psychophysiol 1994;18:49–65.

39. Pascual-Marqui RD. Standardized low-resolution brain electromagnetic tomography (sLORETA): technical details. Methods Find Exp Clin Pharmacol 2002;24:5–12.

40. Pascual-Marqui RD, Lehmann D, Koukkou M, Kochi K, Anderer P, Saletu B, et al. Assessing interactions in the brain with exact low-resolution electromagnetic tomography. Philos Trans A Math Phys Eng Sci 2011;369:3768–84.

41. Fernández-Bouzas A, Harmony T, Fernández T, Ricardo-Garcell J, Santiago E. Variable resolution electromagnetic tomography (VARETA) in evaluation of compression of cerebral arteries due to deep midline brain lesions. Arch Med Res 2004;35:225–30.

42. Grave de Peralta Menendez R, Murray MM, Michel CM, Martuzzi R, Gonzalez Andino SL. Electrical neuroimaging based on biophysical constraints. Neuroimage 2004;21:527–39.

43. Vrba J, Robinson SE. Signal processing in magnetoencephalography. Methods 2001;25:249–71.

44. Biasiucci A, Franceschiello B, Murray MM. Electroencephalography. Curr Biol 2019;29:R80–5.

45. He B, Yang L, Wilke C, Yuan H. Electrophysiological imaging of brain activity and connectivity-challenges and opportunities. IEEE Trans Biomed Eng 2011;58:1918–31.

46. Michel CM, Murray MM. Towards the utilization of EEG as a brain imaging tool. Neuroimage 2012;61:371–85.

47. Plummer C, Harvey AS, Cook M. EEG source localization in focal epilepsy: where are we now? Epilepsia 2008;49:201–18.

48. Michel CM, He B. EEG mapping and source imaging. In : Schomer DL, Silva FH, eds. Niedermeyer’s electroencephalography New York: Oxford University Press; 2018. p. 1135–156.

49. Birot G, Spinelli L, Vulliemoz S, Megevand P, Brunet D, Seeck M, et al. Head model and electrical source imaging: a study of 38 epileptic patients. Neuroimage Clin 2014;5:77–83.

50. Megevand P, Spinelli L, Genetti M, Brodbeck V, Momjian S, Schaller K, et al. Electric source imaging of interictal activity accurately localizes the seizure onset zone. J Neurol Neurosurg Psychiatry 2014;85:38–43.

51. Chowdhury RA, Merlet I, Birot G, Kobayashi E, Nica A, Biraben A, et al. Complex patterns of spatially extended generators of epileptic activity: comparison of source localization methods cMEM and 4-ExSo-MUSIC on high resolution EEG and MEG data. Neuroimage 2016;143:175–95.

52. Hassan M, Mheich A, Biraben A, Merlet I, Wendling F. Identification of epileptogenic networks from dense EEG: a model-based study. Conf Proc IEEE Eng Med Biol Soc 2015;2015:5610–3.

53. Cox BC, Danoun OA, Lundstrom BN, Lagerlund TD, Wong-Kisiel LC, Brinkmann BH. EEG source imaging concordance with intracranial EEG and epileptologist review in focal epilepsy. Brain Commun 2021;3:fcab278.

54. Kim H, Yoo IH, Lim BC, Hwang H, Chae JH, Choi J, et al. Averaged EEG spike dipole analysis may predict atypical outcome in benign childhood epilepsy with centrotemporal spikes (BCECTS). Brain Dev 2016;38:903–8.

55. Alarcon G, Guy CN, Binnie CD, Walker SR, Elwes RD, Polkey CE. Intracerebral propagation of interictal activity in partial epilepsy: implications for source localisation. J Neurol Neurosurg Psychiatry 1994;57:435–49.

56. Shindo K, Ikeda A, Musha T, Terada K, Fukuyama H, Taki W, et al. Clinical usefulness of the dipole tracing method for localizing interictal spikes in partial epilepsy. Epilepsia 1998;39:371–9.

57. Ebersole JS, Hawes-Ebersole S. Clinical application of dipole models in the localization of epileptiform activity. J Clin Neurophysiol 2007;24:120–9.

58. Moon JU, Lee JY, Kim KY, Eom TH, Kim YH, Lee IG. Comparative analysis of background EEG activity in juvenile myoclonic epilepsy during valproic acid treatment: a standardized, low-resolution, brain electromagnetic tomography (sLORETA) study. BMC Neurol 2022;22:48.

59. Lascano AM, Perneger T, Vulliemoz S, Spinelli L, Garibotto V, Korff CM, et al. Yield of MRI, high-density electric source imaging (HD-ESI), SPECT and PET in epilepsy surgery candidates. Clin Neurophysiol 2016;127:150–5.

60. Jonkman LM, Kenemans JL, Kemner C, Verbaten MN, van Engeland H. Dipole source localization of event-related brain activity indicative of an early visual selective attention deficit in ADHD children. Clin Neurophysiol 2004;115:1537–49.

61. Hilli AA, Najafizadeh L, Petropulu AP. A weighted approach for sparse signal support estimation with application to EEG source localization. IEEE Transact Signal Process 2017;65:6551–65.

62. Baroumand AG, Arbune AA, Strobbe G, Keereman V, Pinborg LH, Fabricius M, et al. Automated ictal EEG source imaging: A retrospective, blinded clinical validation study. Clin Neurophysiol 2022;141:119–25.

63. Iachim E, Vespa S, Baroumand AG, Danthine V, Vrielynck P, de Tourtchaninoff M, et al. Automated electrical source imaging with scalp EEG to define the insular irritative zone: comparison with simultaneous intracranial EEG. Clin Neurophysiol 2021;132:2965–78.

64. Dömötör J, Clemens B, Emri M, Puskás S, Fekete I. EEG-based connectivity in patients with partial seizures with and without generalization. Ideggyogy Sz 2019;72:99–109.

65. Tamilia E, AlHilani M, Tanaka N, Tsuboyama M, Peters JM, Grant PE, et al. Assessing the localization accuracy and clinical utility of electric and magnetic source imaging in children with epilepsy. Clin Neurophysiol 2019;130:491–504.

66. Bluschke A, Friedrich J, Schreiter ML, Roessner V, Beste C. A comparative study on the neurophysiological mechanisms underlying effects of methylphenidate and neurofeedback on inhibitory control in attention deficit hyperactivity disorder. Neuroimage Clin 2018;20:1191–203.

67. Adelhöfer N, Gohil K, Passow S, Teufert B, Roessner V, Li SC, et al. The system-neurophysiological basis for how methylphenidate modulates perceptual-attentional conflicts during auditory processing. Hum Brain Mapp 2018;39:5050–61.

68. Hsueh JJ, Chen YZ, Chen JJ, Shaw FZ. Equivalent current dipole sources of neurofeedback training-induced alpha activity through temporal/ spectral analytic techniques. PLoS One 2022;17e0264415.

69. de la Salle S, Phillips JL, Blier P, Knott V. Electrophysiological correlates and predictors of the antidepressant response to repeated ketamine infusions in treatment-resistant depression. Prog Neuropsychopharmacol Biol Psychiatry 2022;115:110507.

70. Bhattacharyya S, Das S, Das A, Dey R, Dhar R. Neuro-feedback system for real-time BCI decision prediction. Microsyst Technol 2021;27:372534.

71. Chen S, He Z, Han X, He X, Li R, Zhu H, et al. How big data and highperformance computing drive brain science. Genom Proteom Bioinform 2019;17:381–92.

72. Li W, Zhang W, Jiang Z, Zhou T, Xu S, Zou L. Source localization and functional network analysis in emotion cognitive reappraisal with EEG-fMRI integration. Front Hum Neurosci 2022;16:960784.

73. Van Eyndhoven S, Dupont P, Tousseyn S, Vervliet N, Van Paesschen W, Van Huffel S, et al. Augmenting interictal mapping with neurovascular coupling biomarkers by structured factorization of epileptic EEG and fMRI data. Neuroimage 2021;228:117652.

74. Val-Calvo M, Álvarez-Sánchez JR, Ferrández-Vicente JM, Díaz-Morcillo A, Fernández-Jover E. Real-time multi-modal estimation of dynamically evoked emotions using EEG, heart rate and galvanic skin response. Int J Neural Syst 2020;30:2050013.

75. Guttmann-Flury E, Sheng X, Zhu X. Channel selection from source localization: a review of four EEG-based brain-computer interfaces paradigms. Behav Res Method 2022 Jul 6. doi: 10.3758/s13428-022-01897-2. [Epub].

76. Yao L, Jiang N, Mrachacz-Kersting N, Zhu X, Farina D, Wang Y. Performance variation of a somatosensory BCI based on imagined sensation: a large population study. IEEE Trans Neural Syst Rehabil Eng 2022;30:2486–93.

77. Khosla A, Khandnor P, Chand T. A comparative analysis of signal processing and classification methods for different applications based on EEG signals. Biocybern Biomed Eng 2020;40:649–90.

78. He B, Coleman T, Genin GM, Glover G, Hu X, Johnson N, et al. Grand challenges in mapping the human brain: NSF workshop report. IEEE Trans Biomed Eng 2013;60:2983–92.

79. Matarasso AK, Rieke JD, White K, Yusufali MM, Daly JJ. Combined realtime fMRI and real time fNIRS brain computer interface (BCI): training of volitional wrist extension after stroke, a case series pilot study. PLoS One 2021;16e0250431.

80. Kawala-Sterniuk A, Browarska N, Al-Bakri A, Pelc M, Zygarlicki J, Sidikova M, et al. Summary of over fifty years with brain-computer interfaces - a review. Brain Sci 2021;11:43.

81. Zander TO, Kothe C, Jatzev S, Gaertner M. Enhancing human-computer interaction with input from active and passive brain-computer interfaces. In : Tan DS, Nijholt A, eds. Brain-computer interfaces Berlin: Springer; 2010. p. 181–199.

82. Landhuis E. Neuroscience: big brain, big data. Nature 2017;541:559–61.

83. Blankertz B, Lemm S, Treder M, Haufe S, Müller KR. Single-trial analysis and classification of ERP components- a tutorial. Neuroimage 2011;56:814–25.

84. Makeig S, Kothe C, Mullen T, Bigdely-Shamlo N, Zhang Z, Kreutz-Delgado K. Evolving signal processing for brain-computer interfaces. Proc IEEE 2012;100:1567–84.

85. Müller KR, Tangermann M, Dornhege G, Krauledat M, Curio G, Blankertz B. Machine learning for real-time single-trial EEG-analysis: from brain-computer interfacing to mental state monitoring. J Neurosci Method 2008;167:82–90.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Publication	Field (s)	Methodology	Study details
Baroumand et al. [62] (2022)	Epilepsy	LORETA	Automated ictal EEG source imaging: a retrospective, blinded clinical validation study.
Moon et al. [58] (2022)	Epilepsy	sLORETA	Comparative analysis of background EEG activity in juvenile myoclonic epilepsy during valproic acid treatment.
Cox et al. [53] (2021)	Epilepsy	sLORETA	EEG source imaging concordance with intracranial EEG and epileptologist review in focal epilepsy.
Iachim et al. [63] (2021)	Epilepsy	sLORETA	Automated electrical source imaging with scalp EEG to define the insular irritative zone: comparison with simultaneous intracranial EEG.
Dömötör et al. [64] (2019)	Epilepsy	LORETA	EEG-based connectivity in patients with partial seizures with and without generalization.
Tamilia et al. [65] (2019)	Epilepsy	Brainstrom	Assessing the localization accuracy and clinical utility of electric and magnetic source imaging in children with epilepsy.
Bluschke et al. [66] (2018)	ADHD	sLORETA	A comparative study on the neurophysiological mechanisms underlying effects of methylphenidate and neurofeedback on inhibitory control in attention deficit hyperactivity disorder.
Bluschke et al. [66] (2018)	Neurofeedback	sLORETA
Adelhöfer et al. [67] (2018)	ADHD	sLORETA	The system-neurophysiological basis for how methylphenidate modulates perceptual- attentional conflicts during auditory processing.
Hsueh et al. [68] (2022)	Neurofeedback	Curry 7	Equivalent current dipole sources of neurofeedback training-induced alpha activity through temporal/spectral analytic techniques.
de la Salle et al. [69] (2021)	Depression	eLORETA	Electrophysiological correlates and predictors of the antidepressant response to repeated ketamine infusions in treatment-resistant depression.

Publication	Field(s)	Study details
Li et al. [72] (2022)	Multimodal techniques	Source localization and functional network analysis in emotion cognitive reappraisal with EEG-fMRI integration.
Van Eyndhoven et al. [73] (2021)	Multimodal techniques	Augmenting interictal mapping with neurovascular coupling biomarkers by structured factorization of epileptic EEG and fMRI data.
Val-Calvo et al. [74] (2020)	Multimodal techniques	Real-time multimodal estimation of dynamically evoked emotions using EEG, heart rate and galvanic skin response.
Guttmann-Flury et al. [75] (2022)	BCI	Channel selection from source localization: A review of 4 EEG-based brain-computer interfaces paradigms.
Yao et al. [76] (2022)	BCI	Performance variation of a somatosensory BCI based on imagined sensation: a large population study.
Bhattacharyya et al. [70] (2021)	BCI	Neuro-feedback system for real-time BCI decision prediction.
Khosla et al. [77] (2020)	Big data	A comparative analysis of signal processing and classification methods for different applications based on EEG signals.
Khosla et al. [77] (2020)	Machine learning
Chen et al. [71] (2019)	Big data	How big data and high-performance computing drive brain science.
Chen et al. [71] (2019)	Machine learning